Computer ScienceComputer Structure

2. 데이터의 종류(진수, 보수, 논리 게이트)

보수

특정 비트의 최대값을 만드는 a+b가 존재한다면, a와 b는 서로 1진 보수 관계다.
2비트의 최대값은 11이다. 10 + 1은 서로 1진 보수다

최대 표현자리 수(modulus)를 형성하는데 서로 보완관계를 이루는 a b를 2진 보수 관계라 한다.
1진 보수에 1 더하면 2진보수다.

쉽게 말하면 a = 0011일때, b가 1진보수면 1100이고, 2진보수면 1진보수에 1더한 1101이 된다.

재밌는 사실은 4비트로 수를 표현한다고 할 때 0=0000이다.
0의 1진보수는 1111이지만, 2진보수는 10000이다. 즉 5비트가 되버린다!!!!
그래서 0의 2진보수는 없도록 설정했고,
총 16가지 숫자 중에 0이 보수가 없으므로, 2진보수는 음수가 하나 더 많다.
(-8은 1000으로 표현, 하지만 8은 4비트로 표현안된다.)
(한편 1진보수는 0의 보수 -0이 존재해서 홀수짝수 갯수가 일치한다.)
1진보수로 표현한 4비트 => (0, 17, -1-7, -0)
2진보수로 표현한 4비트 => (0, 17, -8, -7-1)

보수를 연산에 이용하기(1의 보수 활용)

보수는 뺄셈을 덧셈으로 처리할 수 있다.
32-12 => 32+87(12의 1진보수) = 119이다.
119에서 맨앞 숫자(캐리비트)를 제거하고나서 덧셈하면
즉 19+1 = 20이 된다!

만약 캐리비트가 발생하지 않는 경우는?
32-40
32+59 = 91 여기서 1진보수를 취하고 부호를 바꿔주면 된다!
-9!!

이진수로 해보면,
1011 - 0010 일때,
1011 + 1101
= 11000 여기서 캐리비트를 제거하고 덧셈하면,
1000+0001 = 1001.
즉 1011 - 0010 = 1001이 된다.

1011 - 1110
1011 + 0001 = 1100 여기에 부호를 바꾼 1진보수를 구한다.
1011 - 1110 = -0011

정수

고정 소숫점을 가지는 수.(소수점의 위치가 어디인지 항상 정확하게 인지)
정수도 소숫점을 가진다. 다만 floating하지 않고 고정되어 있을 뿐.

  • 부호화 절대치(signeagnitude) : 부호를 나타내는 비트. 맨 앞 비트가 담당

    • 0이면 양수 1이면 음수
    • +0과 -0이 둘 다 존재하는 한계 => 2진 보수를 활용해서 해결

  • 10진수 정수 표현

    • Unpacked decimal : 1바이트마다 십진수 한 숫자 표현. 입출력용(연산x)
    • Packed decimal : 1바이트마다 십진수 두 숫자 표현. 연산용(입출력x)

소수

부동 소수점을 가지는 수.
총 32비트를 (부호1+지수7+기수20) 이런식으로 분배..

소수를 이진법으로 하기

소수를 나타내려면 일단 2를 곱해서 정수 부분이 해당 소숫점 자리 수가 된다.
그리고 정수부분(캐리비트라고도 한다)을 버린 나머지를 다시 2를 곱해서 반복한다.
이렇게 해서 0이 될때까지 하면 이진법으로 표현된다.

예를 들어 0.625는
0.6252 = 1.25 이므로 소수점 첫자리 수는 1
0.252 = 0.5 이므로 소수점 두번째 자리는 0
0.5* = 1.0 이므로 소수점 세번째 자리는 1
그리고 남은수가 0이므로 과정이 종료되고,
0.625의 이진법 표현은 0.101이 된다!!!

한계

그러나 0.3 같은 수는 이진법 표현식으로는 한계가 있다.
0.6 -> 1.2 -> 0.4 -> 0.8 -> 1.6 -> 0.2…
이렇게 순환반복된다…

이런 상황에서 자료형에 따라 허용된 자리 수까지 표시한다.
즉 정확하게 표시가 안된다!!!!!!!!

BCD 코드

입출력을 위해 10진수를 2진수로 표현해놓은 것.(일일히 2진수로 변환하기 싫어서 만든 것.)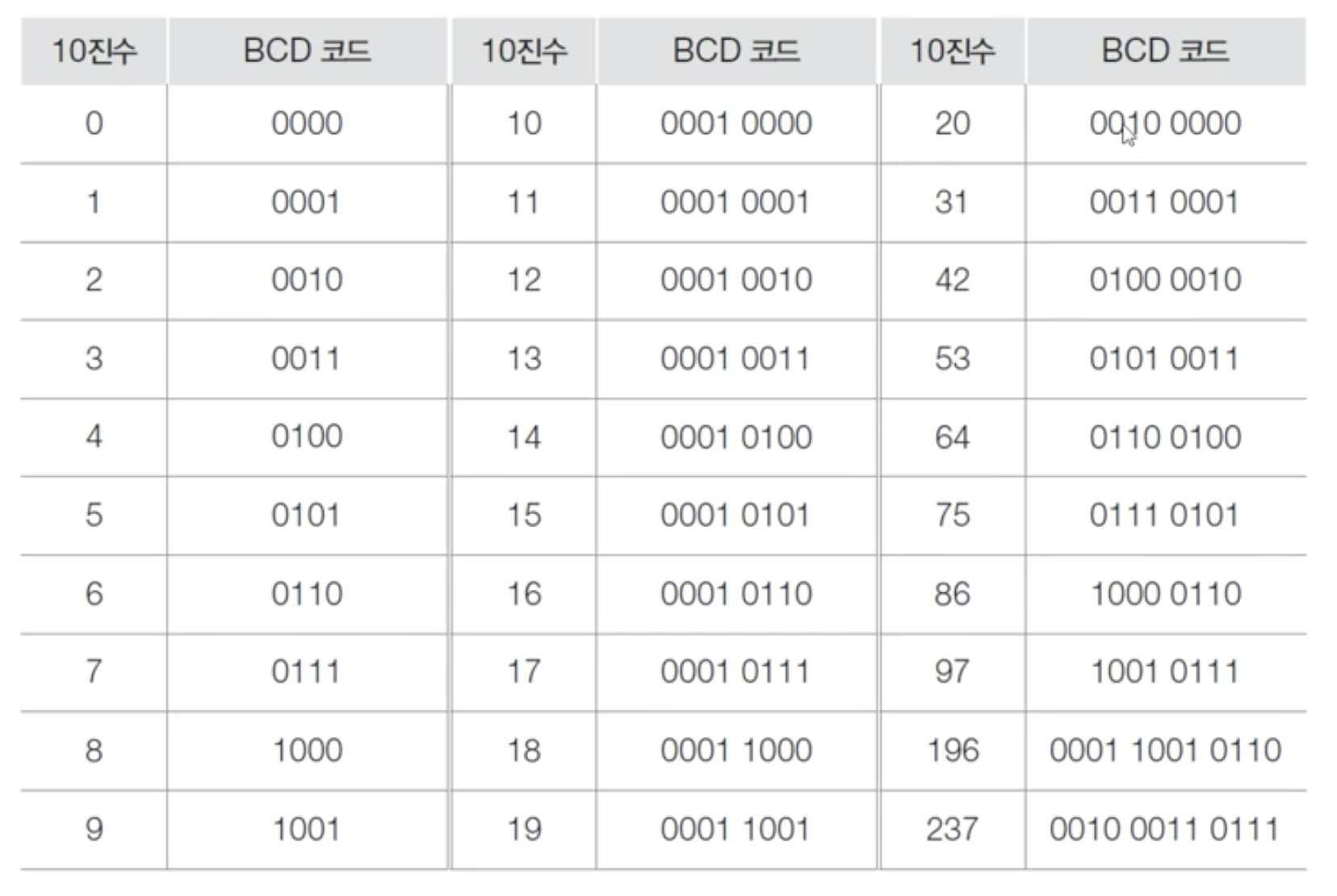

논리 게이트

논리 연산을 수행하는 전자소자.
입력 받은 변수에 따라 정해진 논리 함수를 수행해서 결과값 반환하는 하드웨어

직렬 연결 스위치는? AND 표현과 동치!
병렬 연결 스위치는? OR 표현과 동치!
배타적 논리합(XOR) 서로 값이 다를때 1!

1비트 덧셈 구현 예시

각 1비트인 a,b로
a + b를 구현해보자.

C는 캐리비트고, s는 그 나머지다.
a b C s
0 0 = 0 0
0 1 = 0 1
1 0 = 0 1
1 1 = 1 0

자 이제 a,b,C,s 간 논리 게이트 관계를 따져보자.
C는 a, b가 모두 1일 때 1이다. 즉 a AND b = C
s는 a, b가 서로 다를 때 1이다. 즉 a XOR b = s
결과적으로 보면 논리연산자로 산술적 연산인 덧셈이 표현가능하다는 거다!
이 결과를 논리 게이트로 표현하면 다음과 같다

부울 대수

논리 회로의 형태와 구조를 기술하는 수학적 이론

  1. 교환법칙
    • AB = BA (and)
    • A+B = B+A (or)
  2. 결합법칙
    • A(BC) = (AB)C
    • (A+B)+C = A+(B+C)
  3. 분배법칙
    • A(B+C) = AB+AC
  4. 드모르간 법칙 (부득이하게 여집합을 !로 표현.)
    • !(A+B) = !A!B
    • !(AB) = !A+!B

이 법칙들을 적용해 부울 식을 최대한 간편화 할 수 있다!

조합 논리 회로, 자료 기억 방법, 순차 논리 회로

조합 회로 : 입출력을 가진 논리 게이트의 집합
순차 논리회로는 게이트 뿐만 아니라 기억능력이 있는 플립플롭으로 구성.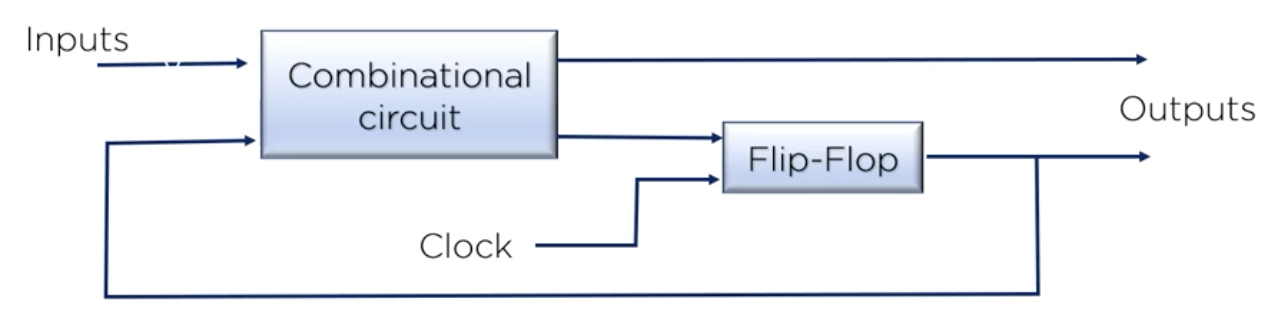

조합 회로가 연산을 수행한다고 할 때, 임시적으로 데이터를 잠깐 저장해야 할 일이 생긴다.
그럴 때 플립플롭에 저장해놨다가 꺼내서 써먹는 방식이다.

대표적인 조합 회로

  • 가산기 : 여러 입력값을 받아 결과물을 출력
  • 멀티플렉서 : 여러 입력 중 하나만 골라서 출력
  • 디멀티플렉서 : 하나의 입력을 여러개의 출력으로 나눠서 보냄

플립플롭 종류와 작동 방식


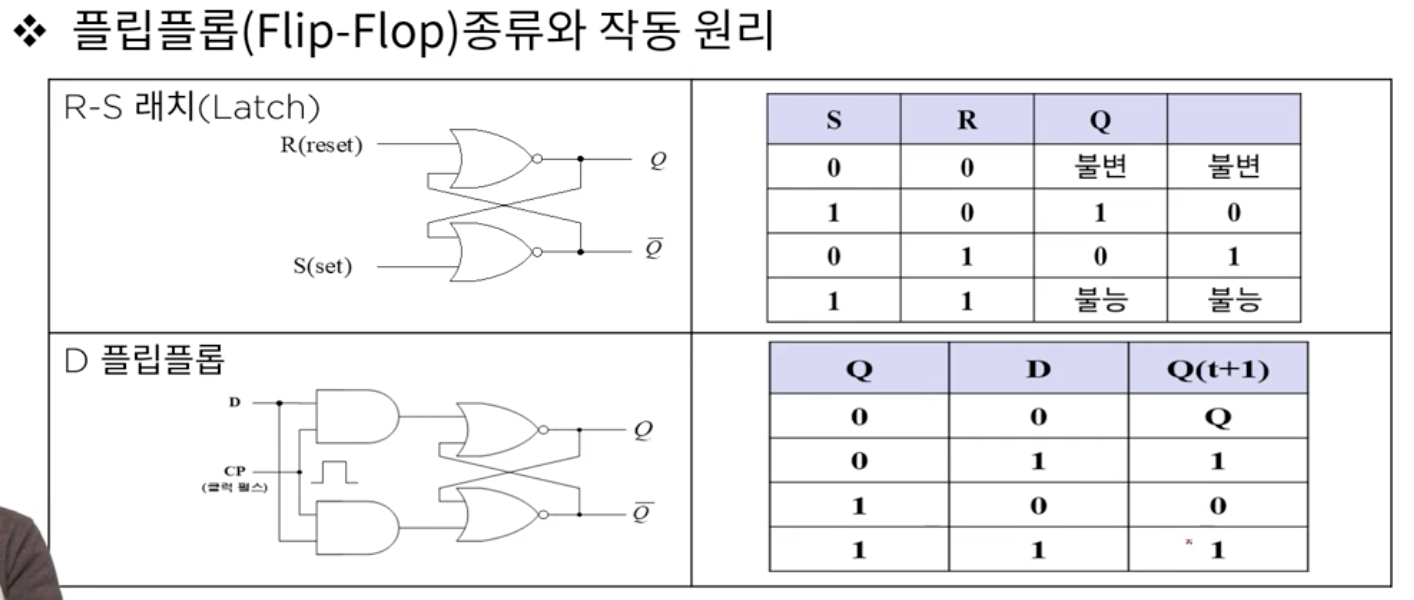
R-S 래치 : 두 값을 받아서 저장하고 수정할 수 있음.
D 플립플롭 : 입력값 D에 따라서 수정, 유지를 할 수 있음

순차회로의 외부 출력은 외부 입력 + 플립플롭 현상태의 함수로 표현

Share