허프만 코딩 문제(Huffman coding problem)
아스키 코드 : 알파벳과 문자들을 0~255개의 숫자로 배정한 것. 즉 8bit로 표현.
이렇게 표현된 8비트의 비트들을 고정길이코드(fixed-length code)라고 한다.
(문자열 100개면 800비트가 필요하게 된다.)
이때 a e i o u 같은 모음들은 빈도수가 높고 q z y는 빈도수가 낮다.
그렇다면, 자주 사용되는 문자의 아스키 코드 비트값은 줄이고, 그렇지 않은 문자들 비트 수는 늘리면 어떨까?
이렇게 변한 길이의 코드를 가변길이 코드라고 하자.
즉 a가 100번, b가 30번, c가 5번이라고 하면,
고정 길이코드로 할 경우, 모두 8비트로 부여할 경우 총 800 + 240 + 40 = 1080 비트가 필요
가변 길이코드로 부여하면, a = 0, b = 101, c = 100으로 할 경우,
100 + 90 + 15 = 205 비트면 충분하게 된다.
하지만 만약 코드를 더 줄이고 싶으면 다음과 같이 하면 된다고 생각할지 모른다.
a = 0, b = 1, c = 10
하지만 그렇게 된다면, 1001010을 baacc 혹은 caabab 등등 해석이 불분명해진다.
따라서 각 문자에 비트를 구분가능하게 부여해야하는데, 이를 prefix-free code라고 한다.
다시 말하면, 각 코드들은 앞부분이 다른 코드와 동일하면 안된다.
(위 예시는 c의 앞부분이 b와 동일했다.)
트리 형태로 생각하기.
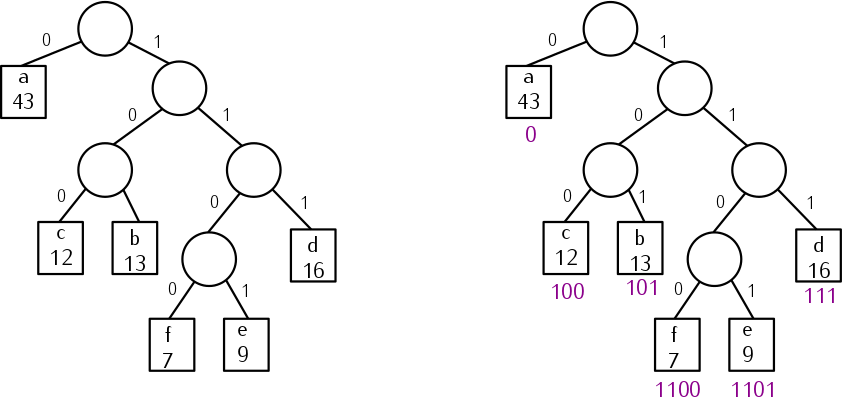
위에서 설명한 규칙들을 기반으로 트리를 만들면 위와 같다.
여기서 짧은 코드를 할당받기 위해서는? 루트노드와 가까워야 한다!
그렇다면 도대체 어떻게 구현한다는 것인가…!!
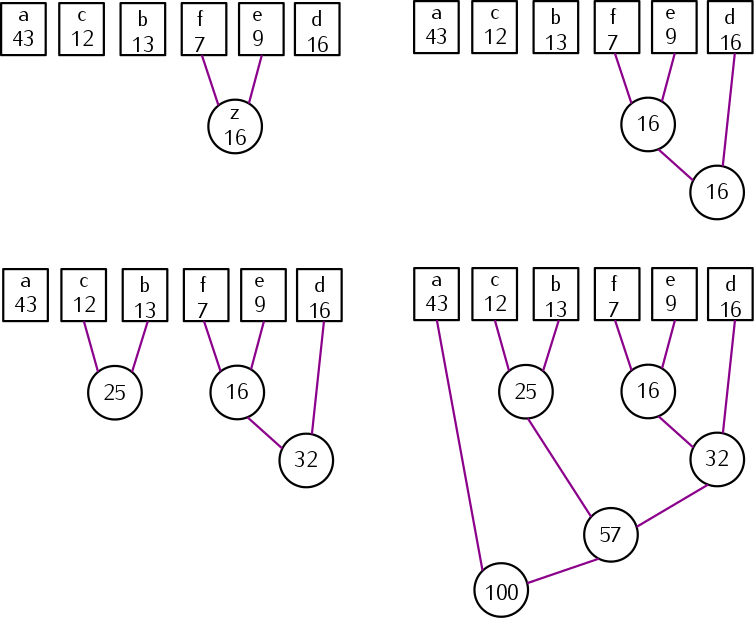
먼저 빈도 내림차로 문자들을 배열에 정렬하여 만들고,(위 사진은 그러지 않았다.)
빈도가 작은 수끼리 빈도를 합쳐가면서 만들면… 우리가 앞서 본 트리와 비슷한 모양이 그려진다.
즉 코드로 구현하려면, 가장 작은 값과 두번째로 작은 값을 찾아 더해야 하는데… 이는 힙으로 구현 가능하다!
이제 우리가 알고싶은 특정 문자열의 총 비용은 모든 문자의 빈도수 X 트리에서 깊이 이다!