LCS(최장공통부문자열) 문제
부문자열은 문자열에서 0개 이상의 문자를 제외하고 남은 문자열을 의미
YANG에서 A를 제외한 YNG같이… 하지만 AGY는 안된다!
공통 문자열은 두개의 문자열의 부문자열이 동일한 것을 말한다!
이 문제는 가장 긴 길이의 공통부문자열을 찾는 문제이다!
Xn 을 x1, x2, x3, … xn 즉 n개의 글자를 갖는 문자열이라고 하고,
**LCS(i, j)**를 Xi와 Yj의 최장공통부문자열의 길이라고 한다면,
xn과 yj(즉 두 문자열의 마지막 글자)가 같은 경우와 그렇지 않은 경우를 생각해야 한다.
만약 마지막 글자가 같으면, 그 글자를 제외하고 생각할 수 있다!
즉 LCS(i, j) = LCS(i-1, j-1) + 1 이런 점화식이 가능하다!
하지만 마지막 글자가 다르다면?
Xi와 Y(j-1). 즉 X전체와 Y에서 마지막을 제외한 문자열의 LCS값과
X(i-1)과 Yj. 즉 X에서 마지막을 제외한 문자열과 Y전체의 LCS값 중 최대값을 구하면된다
즉 LCS(i, j) = max(LCS(i, j-1), LCS(i-1, j))
자 이제 이 점화식을 이차원 리스트로 표현할 수 있다!
if xi==yj LCS[i-1][j-1] + 1
if xi!=yj max(LCS[i][j-1], LCS[i-1][j])
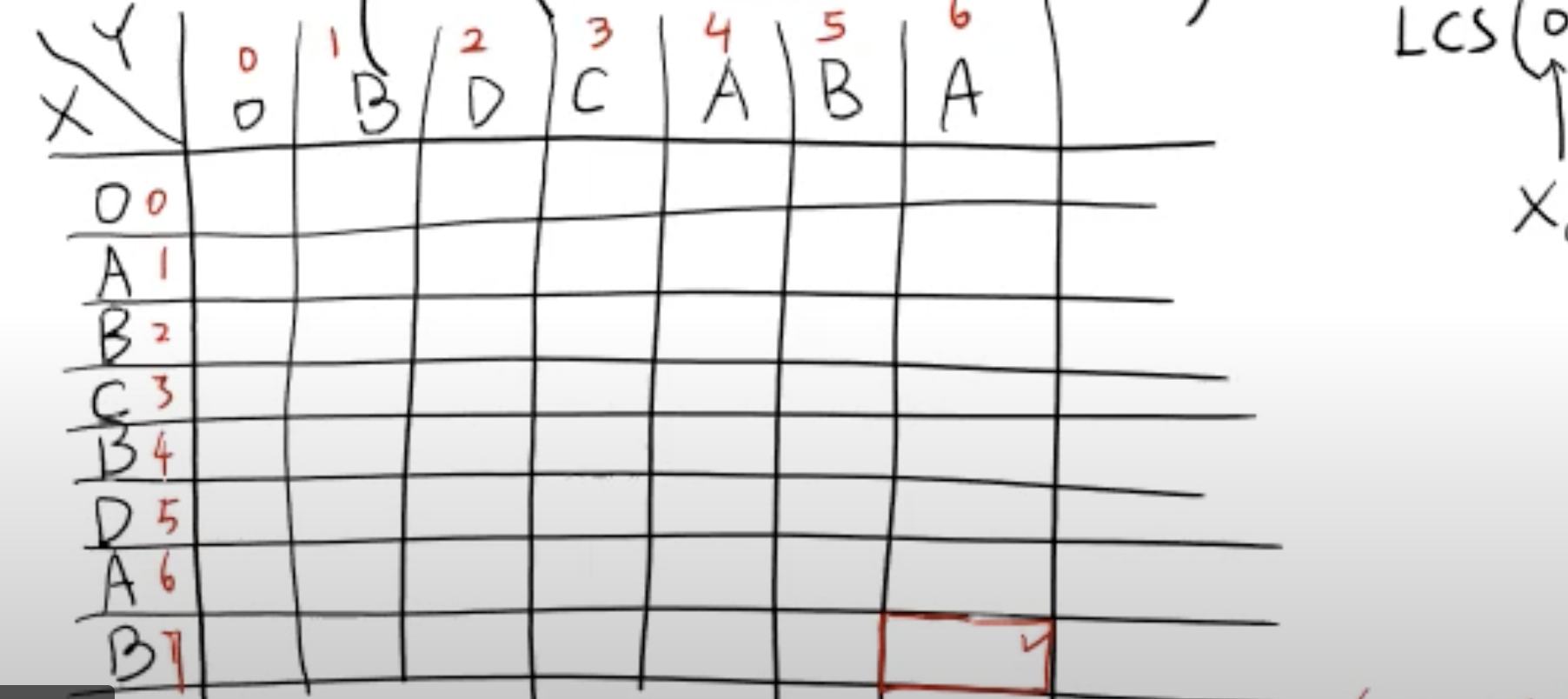
이렇게 대략적으로 테이블이 그려지면, 이제 특이 조건들을 찾아야 된다!
예를 들면 LCS(0,x) 혹은 LCS(x,0) 같은 값들! 이들은 모두 0이다!
그 다음엔, 어떤 절차로 작은 값을 통해 큰 값을 구해낼지 추론해야 한다!
이렇게 테이블을 모두 채우는데 O(mn)의 시간이 걸린다!
만약, 길이가 아닌 문자열 자체를 구하라하면, 테이블을 숫자로 채운 다음, 역으로 추론해가며 올라가자.