Computer ScienceData Structure

9. 그래프

그래프

G = (V, E)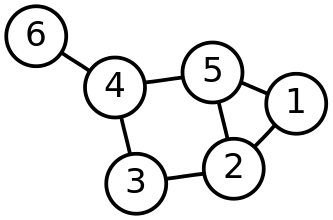

V = vertex set, E = edge set
동그라미가 버택스(혹은 노드), 버택스를 잇는 링크를 엣지라 한다.

degree(분지수) 어떤 노드의 이웃한 노드 갯수.
어떤 그래프의 분지수는 그 그래프의 최대 분지수를 말한다.

인접하다는 의미는 두 노드가 링크로 서로 연결 되어있는 상태를 말한다.

경로는 노드를 중복하지 않고 지나가는 행위
사이클은 노드를 중복하지 않고 출발점으로 다시 돌아오는 경로.

표현법

인접행렬 : 노드 i 와 j에 엣지가 존재하면 G[i][j]=1(혹은 가중치), 없으면 0
인접 리스트 : 1차원 배열 G로 표현, 노드 i에 인접한 노드들은 G[i]에 연결리스트로 표현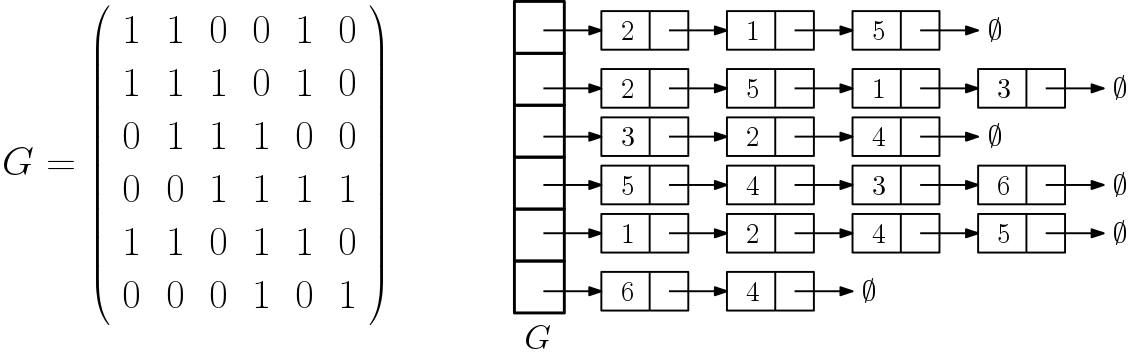

노드 갯수 = n, 엣지 갯수 = m일 때,

  • 인접행렬
    O(n^2)만큼 메모리 사용.
    탐색은 O(1)
    인접한 모든 노드를 보려할때 O(n) 이때 인접노드가 많던 적던 모두 찾음
    노드 삽입은 O(1)
    노드 삭제는 O(1)

  • 인접리스트
    O(n+m)만큼 메모리 사용.
    탐색은 O(n)
    인접한 모든 노드를 보려할때 O(n) 이때 인접노드가 적으면 연산도 짧아짐.
    노드 삽입은 O(1)
    노드 삭제는 O(n)

대부분 인접행렬은 상수 시간에 연산을 완료한다. 메모리 측면은 인접리스트가 유리하다.

그래프 순회

그래프에는 DFS(깊이 우선 탐색), BFS(너비 우선 탐색) 두가지 방법이 존재한다.

DFS

방문한 노드와 연결된 이웃 노드 중 아직 방문하지 않은 노드가 있으면 그 노드를 다음에 방문.
만약 안가본 노드가 없다면 방문하기전 노드로 가서 다시 검사한다.
재귀함수로 작성하는게 일반적.


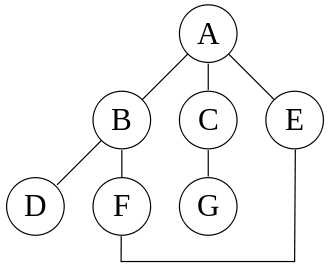
이런 그래프에서 a부터 알파벳 순서가 빠른 노드부터 방문한다고 하면
A-B-D-F-E-C-G

pseudo code로 이해해보자

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def DFS(V):
    mark V as visited node #visited[V] = True
    pre[V] = curr_time #record the first visiting time
    curr_time +=1
    for each edge(V, W): #for all neighbor node
        if w is unmarked:
            parent[W] = V
            DFS(W)
    post[V] = curr_time #V에서 DFS완료된 시간
    curr_time+=1
def DFSALL(G):
    for all nodes in G:
        mark[V]= unvisited
    for all nodes V:
        if mark[V]!=visited :DFS(V)

pre는 해당 노드에 처음 방문한 시간, post는 해당 노드에서 DFS가 완료된 시각(모든 이웃을 이미 방문).
parent 리스트를 활용해서 트리 모양으로 그래프를 표현할 수 있다.

재귀를 사용하지 않고 스택을 통해 구현할 수 있다.

1
2
3
4
5
6
7
8
9
10
def DFS(s): #s 부터 DFS시작.
    stack.push((None, s)) #(부모노드, 현재 방문노드) 튜플을 추가
    while stack is not empty:
        p, v = stack.pop()
        if v in unmarked: 
            mark[v]= visited
            parent[v] = p
            for each edge(v, W):
                if w is unmarked:
                    stack.push((v,w))

노드의 엣지가 방향성을 갖는 방향 그래프도 알아두자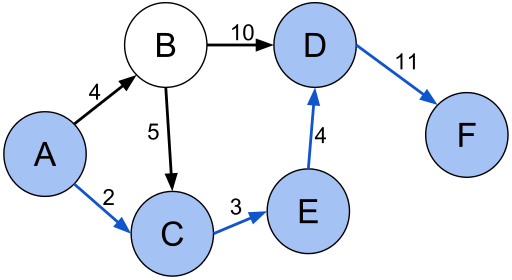

BFS

BFS는 루트노드-루트의 이웃 - 이웃의 이웃… 이런 식으로 level by level로 방문한다.
queue 자료구조로 비재귀 코드로 작성하는게 일반적이다.

이런 그래프에서 방문 순서는 다음과 같다
(A)-(B-C-E)-(D-F-G)

psuedo code로 보자

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def BFS(G = (V,E)):
    #node 0에서 시작.
    #n은 노드의 갯수
    visited = [False]*n
    parent = [-1]*n
    dist = [0]*n
    Q = Queue()
    for all source node s in G:
        Q.enqueue(s)
        while Q is not empty:
            v = Q.dequeue() #dequeue는 방문을 의미
            visited[v] = True
            for each edge v.neighbor w:
                if no visited[w]:
                    Q.enqueue(w)
                    parent[w] = v
                    dist[w] = dist[v] +1

출발 노드에서 다른 노드 v까지의 최단 경로 길이는 dist[v]에 저장.

Share