Computer ScienceData Structure

8. 균형이진탐색트리

균형이진탐색트로(BST)?

이진트리는 search, insert, delete 연산들이 O(h) 시간이 걸린다는 걸 기억하자.

즉 이 연산들을 효율적으로 하려면 트리의 높이를 최소화해야 한다.
이진트리에서 빼곡히 노드를 채워넣어 높이를 최소로 하면 대략 log n 정도가 되는데,
균형이진탐색트리는 노드를 최대한 채워넣어 높이를 log n이 되도록 유지하는 자료구조다!

트리의 높이를 최소화하는 rotation 회전 연산

한쪽의 서브트리가 지나치게 아래로 치우쳐져있으면,
해당 서브트리에서 반대쪽 서브트리로 회전을 시켜서 전체 트리 높이를 낮춘다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
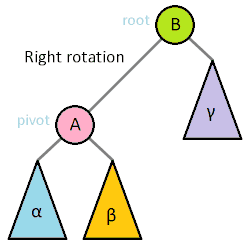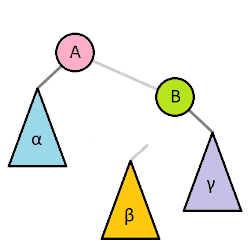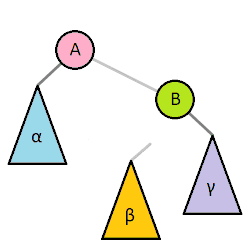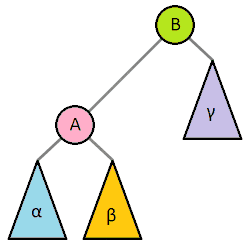
22
def rotateRight(self, z): 
    # left도 가능, z가 최상위 노드 x가 올라가는 노드
    if not z = return
    x = z.left
    if x == None:return #이런 경우, left로 회전해야...
    b = x.right
    
    x.parent = z.parent #x를 맨위 노드로...
    if z.parent: #만약 z의 부모가 존재하면 부모와의 관계를 x로 다 바꿈
        if z.parent.left == z:
            z.parent.left = x
        else:
            z.parent.right = x
    if x: x.right = z #최상위 노드가 x가 됐으니, 이제 z와 x의 관계를 설정
    z.parent = x
    
    z.left = b #x의 오른쪽 서브트리가 z의 왼쪽 서브트리가 됨
    if b : b.parent = z #b와 z의 관계를 새롭게 설정

    #만약 z가 루트노드인 경우.
    if z == self.root and z != None:
        sefl.root = x

AVL 트리

균형이진트리의 일종.

모든 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차가 1 이하인 이진탐색트리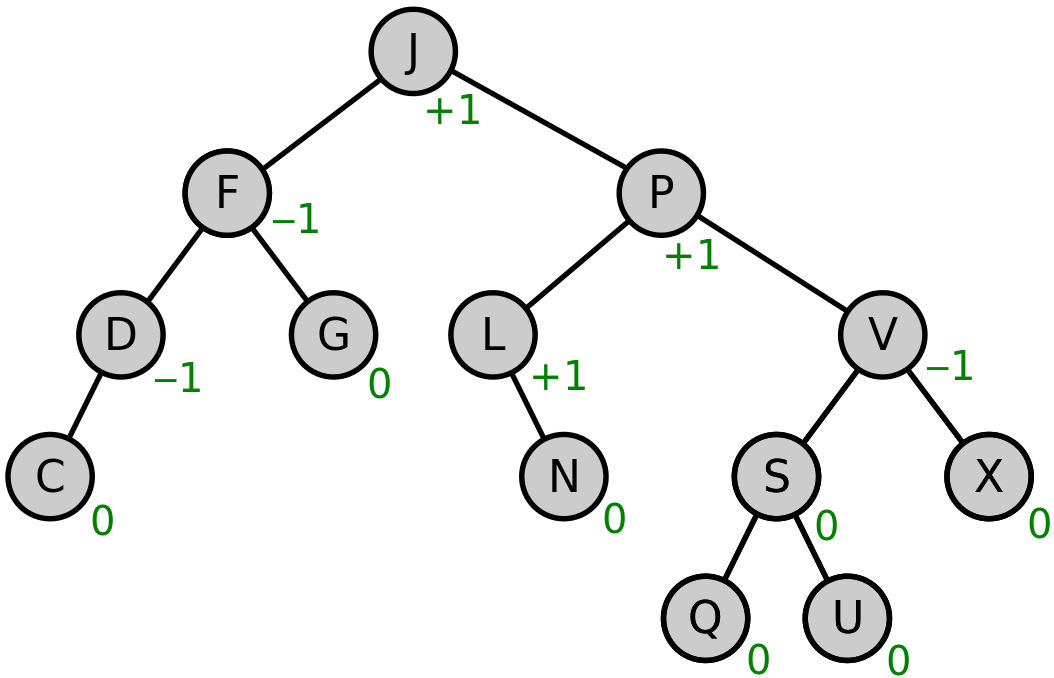

AVL 트리에서 삽입/삭제하면, 서브트리 높이 차가 1보다 커지는 경우 발생 가능..

이럴 경우, 회전연산을 통해 높이를 다시 맞춰야 함.(rebalance)

AVL은 BST의 일종이므로, BST의 Node 클래스에 height를 추가한 노드 클래스를 사용한다.

class AVL(BST): #상속
    def insert(self,key):
        v = super(AVL, self).insert(key) # BST클래스의 insert 함수 호출

삽입 insert(key)

  1. v = super(AVL, self).insert(key) 로 BST에서 정의한 insert를 실행
  2. 삽입연산에 따라 균형이진탐색트리의 균형이 무너졌을 경우, 삽입 위치부터 올라가며, 무너진 곳을 순서대로, x y z로 함.
  3. 트리의 균형을 맞추는 rebalance연산을 실행하고 원래 z의 자리에 올 노드를 w로 하자.
  4. rebalance 연산은 x y z의 형태에 따라 달라짐.




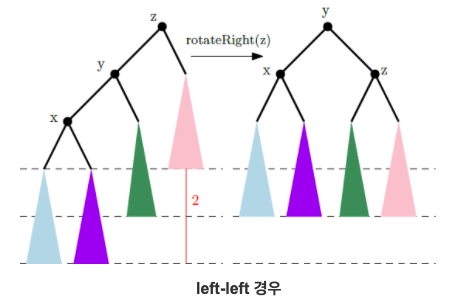
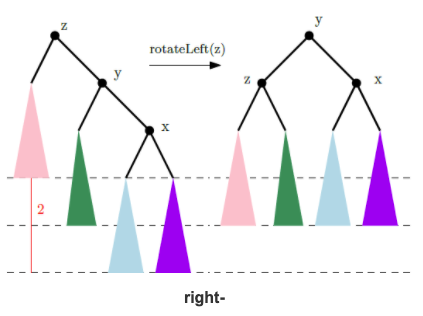
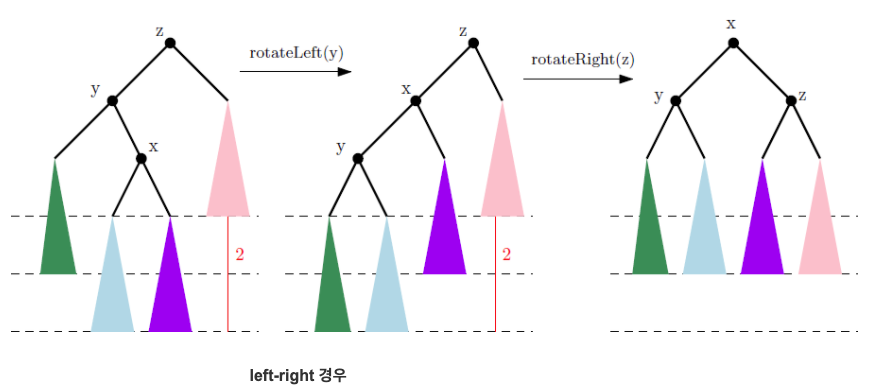
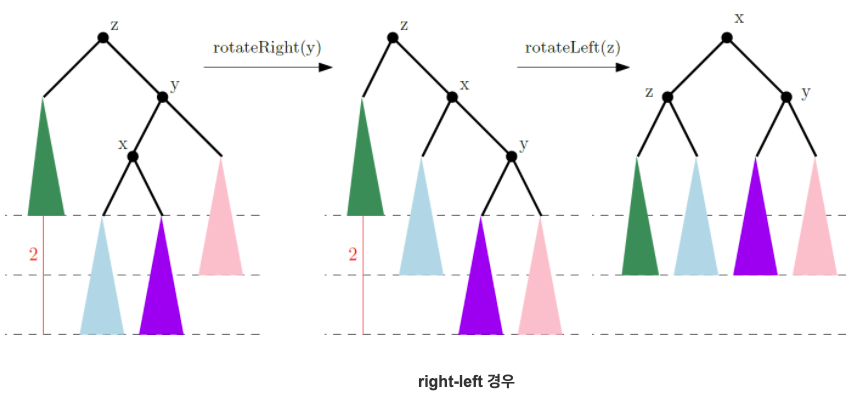
  1. 만약 w가 루트노드라면, self.root=w을 해주자.

결과적으로 O(log n)이다.

삭제 delete(u)

  1. v = super(AVL, self).deleteByCopying(u) 이때 삭제연산은 삭제하고 나서 삭제된 노드의 부모를 반환한다.
  2. v가 None이 될 때까지 루프.
  3. 만약 v가 균형이 깨지지 않았다면, v의 부모노드가 v가 된다.
  4. 만약 v가 균형이 깨진다면, v 위치 노드를 z로 하고, z의 자식 중, 깊이가 더 큰 쪽 노드를 y, y의 자식 중 깊이가 더 큰 쪽 노드를 x라 한다.
  5. 이제 rebalance 연산을 한다. x<\y<\z 일 경우 로테이션 한번, x>y&&z>y일 경우 로테이션 두번 한다.


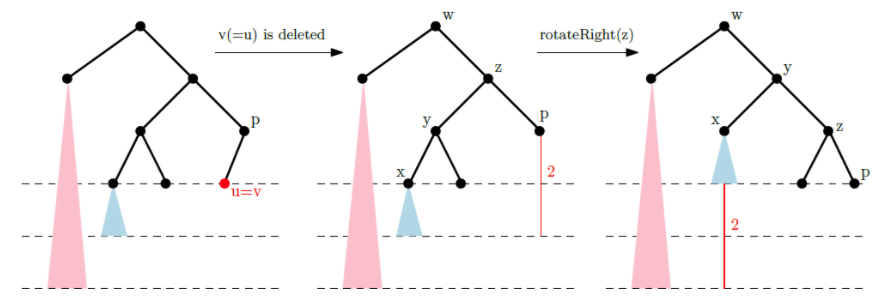
6. 로테이션 후, 원래 z의 위치에 오는 노드를 v라 한다.
7. 이제 v의 트리는 균형을 성공했지만, v의 부모 노드로 가서 동일한 과정을 해야 한다.
8. w = v, v=v.parent로 하여 w는 v의 자식 노드가 되고, v는 위쪽으로 한칸 가서 동일한 작업을 한다.

결과적으로 최약의 경우에는 회전연산(상수시간)을 log n번 하게 되어, O(log n)이다.

Share