7. 힙

2021-07-28

2022-01-23

힙

힙을 알기 위해서는 트리에 대한 기본적인 지식이 필요하다.

힙의 특성

어떤 특정 값을 찾아내는 기능은 지원하지 않지만,
값을 삽입하고, 최대값(최소값)을 찾거나 삭제하는데 큰 강점을 가진 자료구조.
만약 최소값을 찾거나 삭제하고 싶으면 힙성질을 반대로 설정하면 된다.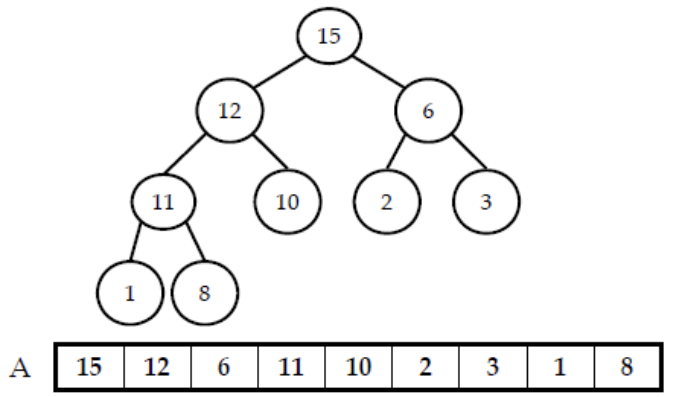
heap2

간단한 용어 설명

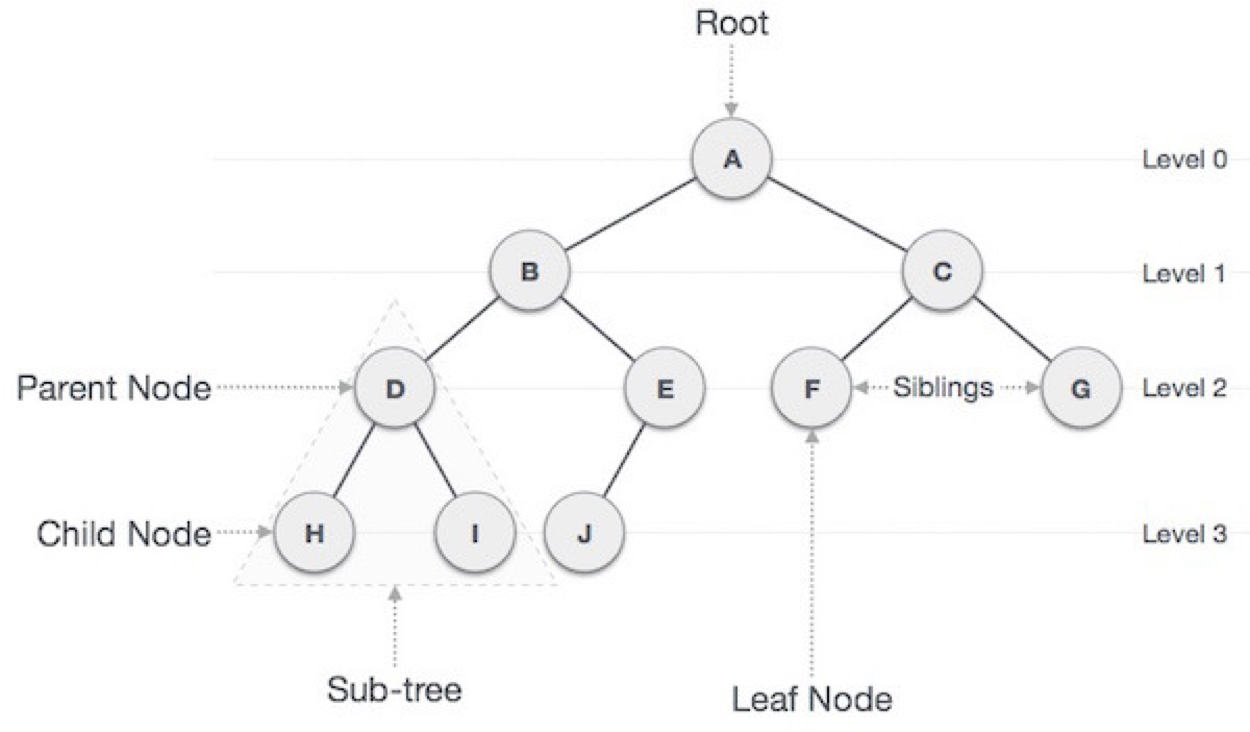
heap1

트리 표현법

표현법 1:
level 0 부터 해당 노드 자리에 노드가 있으면 노드이름을 쓰고, 없으면 None이라고 써서 가능한 모든 자리만큼 원소를 갖는 리스트로 표현.
표현법 2:
트리의 수직적 관계를 리스트 속 리스트를 활용해 표현하기. [부모노드, [부모노드의 왼쪽 서브트리], [부모노드의 오른쪽 서브트리]]. 이때 빈 노드나 서브트리는 빈 리스트 []로 표현한다.
표현법 3: 노드 클래스 활용
각 노드를 노드클래스로 구현해서 객체를 부여해 구현.

힙이란?

힙이란 1차원 배열 중 저장된 값이 힙 조건에 만족하는 배열을 의미.

힙조건

힙 조건에는 크게 모양 조건과 값 조건이 있다.

모양 조건 : 리스트(배열)을 이진트리로 해석했을 경우.

마지막 레벨을 제외한 각 레벨엔 빠짐없이 노드가 존재한다.
마지막 레벨의 노드는 왼쪽부터 차례대로 빈틈없이 채워진다.

값 조건

루트 노드를 제외한 모든 노드의 값은 부모 노드의 값보다 크지 않아야 한다!!
(또는 각 노드의 값은 자신의 자손 노드들의 값보다 같거나 커야 한다.)

인덱스 값 구하기

힙 조건을 만족하는 배열(리스트)A의 노드 A[k]가 있을 때,

왼쪽노드 : A[2k+1]
오른쪽노드 : A[2k+2]
부모노드 : A[(k-1)/2]

이렇게 왼쪽, 오른쪽, 부모 노드의 인덱스를 구할 때는 O(1)의 복잡도를 가진다.

힙 값 조건을 만족시키도록 만드는 연산

힙이 될려면, A[k]가 자신의 자식 노드들과 같거나 커야한다.

이를 위해 A[k]를 자식노드와 비교 하면서 더 큰 자식을 찾으면 서로 swap해줘야 한다.(인덱스로 하면 된다.)

이 과정을 더이상 할 필요가 없을때까지 반복하면 힙의 값 조건을 만족하게 된다.

def heapify_down(self, k, n):
    while 2*k+1<n:
        L,R = 2*k+1 , 2*k+2
        if L<n and self.A[L] > self.A[k]:
            m=L
        else:
            m = k
        if R<n and self.A[R] > self.A[m]:
            m = R
        if m != k:
            self.A[k], self.A[m] = self.A[m], self.A[k]
            k = m
        else : break
def make_heap(self):
    n = len(self.A)
    for k in range(n-1, -1, -1):
        self.heapify_down(k, n)

heapify_down 연산은 O(힙의 높이)이고, make_heap의 연산은 heapify_down연산을 n번 하는 것이므로 O(n*힙높이)이다.

힙의 높이와 힙 원소 갯수 사이의 관계

힙의 높이를 h라고 하고 원소 갯수 n개라고 했을 때,

레벨 0 :1개 / 레벨 1: 2개 / 레벨 3: 4개 …..레벨 h-1 : 2^(h-1) / 레벨 h : 최소 1개 이다.

즉 1+2+4+8+….2^(h-1)+1 <=n 이 되고,

(2^h -1) / (2-1) + 1 <= n

2^h-1+1 <= n

2^h<=n

h <= logn 이라는 관계가 성립한다.

이 관계를 토대로 heapify_down 과 make_heap 연산을 보면,

heapify_down은 O(log n), make_down은 O(nlog n) 엄밀히 말하면 O(n)이다. 이 된다.

힙 정렬

힙 조건을 만족하는 배열을 정렬시키는 방법.

주어진 배열 A가 힙일 경우, 힙의 루트 노드에는 항상 전체의 최대값이 저장되어 있다
루트 노드의 값(현재 최대값) A[0]을 현재 리스트의 가장 마지막 값과 바꾼다.
새로 루트 노드에 온 값은 힙 성질을 만족하지 않을 수 있다.
루트 노드를 heapify_down 을 통해 힙의 위치를 찾아가도록 한다.
위 과정을 (n-1)번 반복하면 (n-1)개가 정렬되어 모든 n이 정렬된다.

def heap_sort(self):
    n = len(self.A)
    for k in range(len(self.A)-1, -1, -1):
        self.A[0], self.A[k] = self.A[k], self.A[0]
        n = n -1
        self.heapify_down(0, n)

heap_sort의 수행시간은 루트노드와 마지막 리프노드 자리바꾸고 heapify를 (n-1)번 하므로, (n-1)*O(log n) = O(nlog n)

힙 삽입

일단 삽입할 값을 리프노드로 넣고, 힙 성질에 맞는 위치로 가도록 올려보내는 것.

일단 힙 성질에 맞는 위치로 가는 heapify_up 함수를 만들어 insert함수에 적용시키도록 해보자!

def heapify_up(self, k):
    while k>0 and self.A[(k-1)//2 ] < self.A[k] :
        self.A[k], self.A[(k-1)//2] = self.A[(k-1)//2], self.A[k]
        k = (k-1)//2
def insert(self, key):
    self.A,append(key)
    self.heapify_up(len(self.A)-1_

insert의 수행시간은 O(h=log n) 시간이 걸린다.

최대값을 찾고 삭제하기

이전에도 여러번 말했듯이, 힙에서 최대값은 바로 루트노드다!
최대값을 찾는다면 그냥 A[0]을 반환하면 된다! 참 쉽다!

근데 최대값을 삭제하는건 좀 까다롭다.
최대값을 삭제하고 나서도 힙을 유지하려면 약간의 조정이 필요하기 때문이다.

최대값 삭제

일단 최대값을 삭제하려면 루트 노드를 지우고, 맨 마지막 리프노드를 루트 노드 자리에 둔다.
그러면 당연히 힙 조건을 벗어나게 되는데, heapify_down 연산을 통해 힙 성질을 만족시킨다!

def delete_max(self):
    if len(self.A) == 0 : return None
    key = self.A[0]
    self.A[0], self.A[len(self.A)-1] = self.A[len(self.A)-1], self.A[0]
    self.A.pop()
    heapify_down(0, len(self.A))
    return key

최대값 삭제의 경우, 루트노드와 마지막 노드 자리바꾸고 heapify_up하므로 O(h = log n) 시간이 걸린다.

수행시간 정리

heapfify_up, heapify_down : O(log n)
make_heap : O(n log n) -> O(n)
insert : O(log n)
delete_max : O(log n)
heap_sort : O(n log n)

mudura

Computer ScienceData Structure