6. 이진트리

2021-07-28

2022-01-23

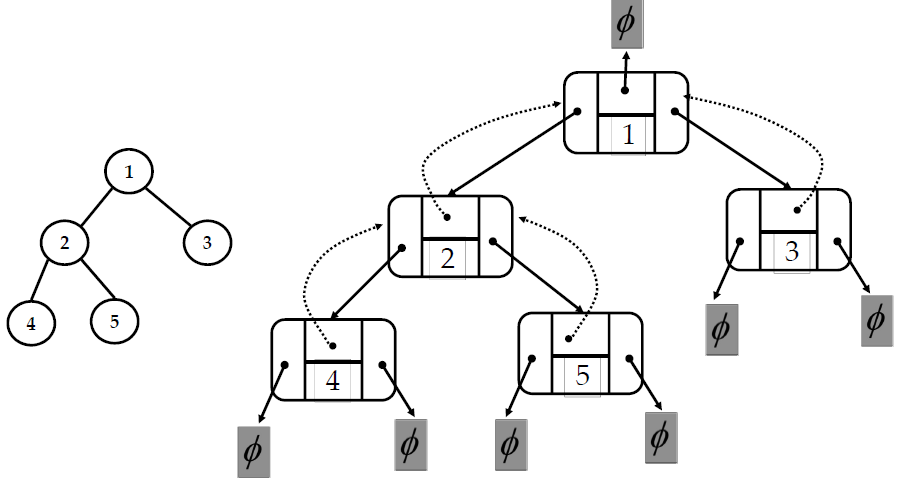
이진트리?

자식노드가 최대 2개 뿐인 트리를 이진트리라 한다!!

class Node:
    def __init__(self, key, parent=None, left=None, right=None):
        self.key = key
        self.parent = parent
        self.left = left
        self.right = right
        
    def __str__(self):
        return str(self.key)
    
class Tree:
    def __init__(self):
        self.root = None
        self.size = 0

이진트리의 순회

이진트리 노드 key값을 빠짐없이 출력하는 방법!

preorder
inorder
postorder

헤더 노드를 M, 왼쪽 서브트리를 L, 오른쪽 서브트리를 R이라고 가정!

쉽게 생각하면 L, M, R이 삼각형 모양으로 있을 때 우선순위 노드가 있으면 해당 노드를 먼저 탐색하는 방식이다!

preorder

MLR 순으로 방문하는 방식
FBADCEGIH 순으로 방문하게 된다!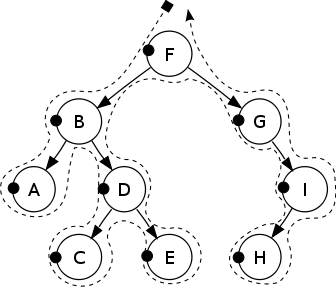

inorder

LMR 순으로 방문하는 방식
ABCDEFGHI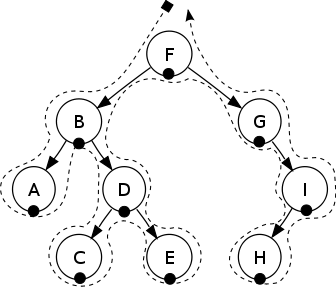

postorder

LRM 순으로 방문하는 방식
ACEDBHIGF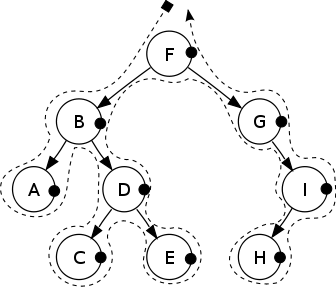

코드로 구현하기

class Node:
    def __init__(self, key, parent=None, left=None, right=None):
        self.key = key
        self.parent = parent
        self.right = right
        self.left = left
    
    def __str__(self):
        return str(self.key)
    
class Tree:
    def __init__(self):
        self.root = None
        self.size = 0
    def preorder(self, v):
        if v:
            print(v.key, end=' - ')
            self.preorder(v.left)
            self.preorder(v.right)
    ''' inorder는?
        if v:
            self.inorder(v.left)
            print(v.key, end=' - ')
            self.inorder(v.right)
        postorder는?
        if v:
            self.postorder(v.left)
            self.postorder(v.right)
            print(v.key, end=' - ')
        
        즉 재귀 알고리즘을 활용하여 print문의 위치를 바꿔가면서 구현하는거다!!!'''

이진탐색트리 BST

이진트리 중에 가장 많이 쓰이는 트리!
이진트리의 노드를 search할 때 효율적으로 할 수 있게!

특징

각 노드의 왼쪽 서브트리의 key값은 노드의 key값보다 작거나 같아야 한다.
반면 오른쪽 서브트리의 key값은 노드의 key값보다 작거나 같아야 한다.

이런 특징이 탐색이 효율적으로 되게 한다!
이진트리의 탐색 연산은 O(h=트리 높이)이므로, 만약 이진트리의 강점을 극대화하고 싶으면, 트리의 높이를 최소화 하는 방향으로 설계해야 한다!

코드로 구현

class BST:
    def __iniit__(self):
        self.root = None
        self.size = 0
    def __len__(self):
        return self.size
    def __iter__(self):
        return self.root.__iter__()

탐색 함수 search와 삽입 함수 insert

탐색 함수와 삽입함수를 구현하기 전에, 해당 노드가 있다면, 해당 노드를 반환하고, 없다면 노드가 삽입될 위치의 부모노드를 반환하는 find_loc 함수를 먼저 구현해보자!

def find_loc(self, key):
    if self.size == 0: return None
    p = None
    v = self.root
    while v != None:
        if v.key == key : return v
        elif v.key < key :
            p = v
            v = v.right
        else :
            p = v
            v = v.left
    return p

이제 find_loc함수를 활용해 search함수를 만들어보자!

def search(self, key):
    v = self.find_loc(key)
    if v and v.key==key:
        return v
    else :
        return None

노드를 삽입하는 insert함수도 만들 수 있다!

def insert(self, key):
    v = Node(key)
    if self.size==0 : self.root = v
    else :
        p = self.find_loc(key)
        if p and p.key != key:
            if p.key < key: p.right = v
            else : p.left = v
            v.parent = p
    self.size += 1
    return v

여기서 잠깐 생각해보자. 만약 삽입 연산을 한다고 할 때, 삽입 순서에 따라 트리 모양도 달라질 수 있을까?

find_loc, insert, search의 수행시간

search, insert 모두 find_loc의 수행시간과 동일하다. (그 외 연산은 모두 상수시간에 이뤄지니까)
find_loc은 최악의 경우 트리의 높이 만큼 수행시간이 걸리므로, O(h) 이다.

삭제 함수 delete

이진 트리에서는 크게 두가지 방법이 있다.

delete by merging
delete by copying

delete by merging

어떤 노드를 지우게 되면 그 노드의 왼쪽 서브트리가 지운 노드의 자리에 오고 지운 노드의 오른쪽 서브트리는 왼쪽 서브트리의 자식 노드가 된다!

이때 삭제할 노드가 루트노드인 경우와 그렇지 않은 경우 두가지로 나뉜다.

삭제할 노드를 x, 왼쪽 자식노드 a, 오른쪽 자식노드 b, x의 왼쪽 서브트리중 가장 큰 노드 m이라 하고 x의 부모노드를 pt라고 하자.

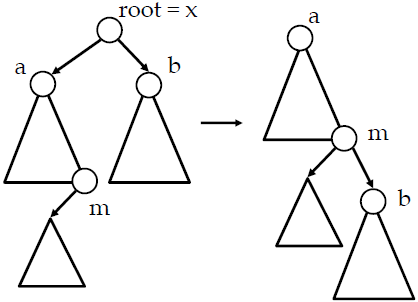
만약 삭제할 노드가 루트노드일 경우

m이 존재 할 경우(if a!=None) : b가 m의 오른쪽 자식노드가 되도록 링크 수정, a가 루트노드가 되도록 변경
a == None이면 : b가 새로운 루트노드가 됨

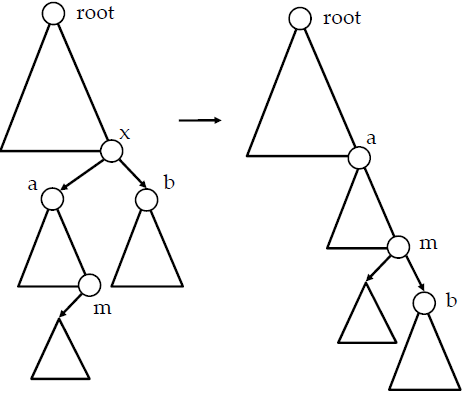
만약 삭제할 노드가 루트노드가 아닌 경우

m이 존재 할 경우(if a!=None) : b가 m의 오른쪽 자식노드가 되도록 링크 수정, a가 pt의 자식노드가 되도록 변경
a == None이면 : b가 pt의 자식노드가 되도록 변경

코드로 구현해보자

def deleteMerging(self, x) {
    a, b, pt = x.left, x.right, x.parent
    if a == None: c = b
    else:
        c = m = a
        while m.right:
            m = m.right
        m.right = b
        if b: b.parent = m

    if self.root == x : #c가 새로운 루트노드가 된다.
        if c: c.parent = None
        self.root = c
    else :
        if pt.left == x : pt.left = c
        else: pt.right = c
        if c: c.parent = pt
    self.size -= 1
}

delete by copying

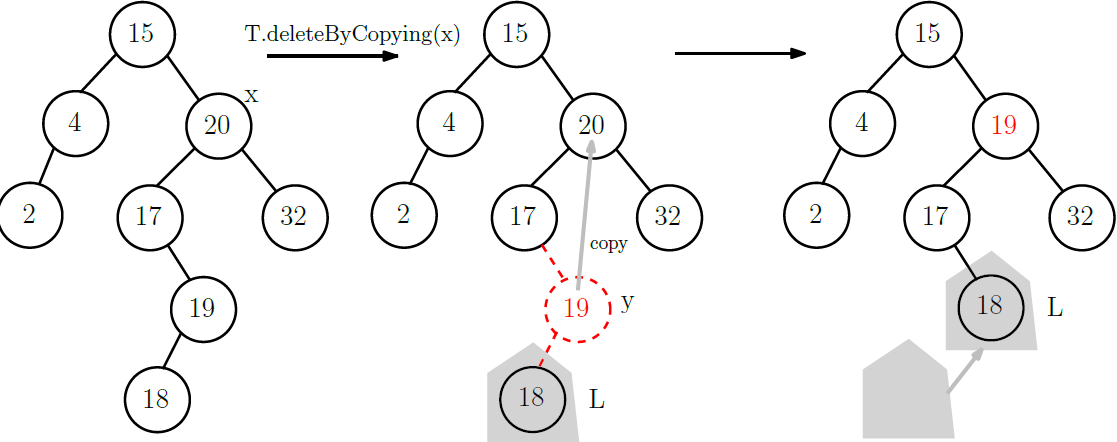
어떤 노드 x를 삭제하려 할 때, 왼쪽 서브 트리를 L, 오른쪽 서브 트리를 R이라고 하자.

L에서 가장 큰 노드 y를 찾는다.
y의 key 값을 x의 key값으로 카피한다.
y의 왼쪽 서브트리가 존재하면, y의 자리로 옮긴다.

코드로 만들어보자

def deleteByCopying(self, x){
    L, R = x.left, x.right
    if L == None :
        x.key = R.key
        if R.right:
            x.right = R.right
        R = None
    else :
        m = L
        while m.right:
            pt = m
            m = m.right
        x.key = m.key
        if m.left:
            pt.right = m.left
            m.left.parent = pt
        m = None
}

delete by merging, delete by copying 의 수행 시간

두 연산 모두 지우려는 노드의 왼쪽 서브트리에서 가장 큰 노드 m을 찾는 연산이 중요.

두 경우 모두 최악의 경우 트리의 높이까지 m을 찾아야 하므로, O(h)이다.

mudura

Computer ScienceData Structure