4. 해쉬테이블

2021-07-28

2022-01-23

a. 해시테이블

해시 테이블은 일종의 정보를 저장하는 서랍장.

a는 2층에 b는 3층에 c는 1층에 넣어두는 방식…
b를 보고 싶으면 어떤 서랍에 넣었는지 알아내서, 3층 서랍에 있는 내용 중에 b와 일치하는 것을 찾는 것.

해시테이블은 삽입, 삭제, 검색 연산을 빨리 처리할 수 있다.

만약 순서대로 정보를 서랍장에 넣었을 경우, 어떤 정보를 찾으려 할 때 일일히 순차적으로 찾아야 된다.

하지만 해시테이블은 그런 식으로 연산하지 않는다. 바로 해시 함수라는 것을 이용하기 때문에 보다 빠른 연산속도를 갖는다.

해시테이블 자료구조에서 가장 핵심은 각 정보들을 어떤 서랍에 넣을지를 결정하는 것!!!

정보를 어떤 서랍장(슬롯)에 넣을지를 결정하는 것이 바로 해시 함수!!!(f()로 표현)

예를 들어, 해시 테이블 H를 int H[10]으로 선언해 사용한다고 하자
해시 함수는 f(K) = K % 10로 정의했다고 하자.
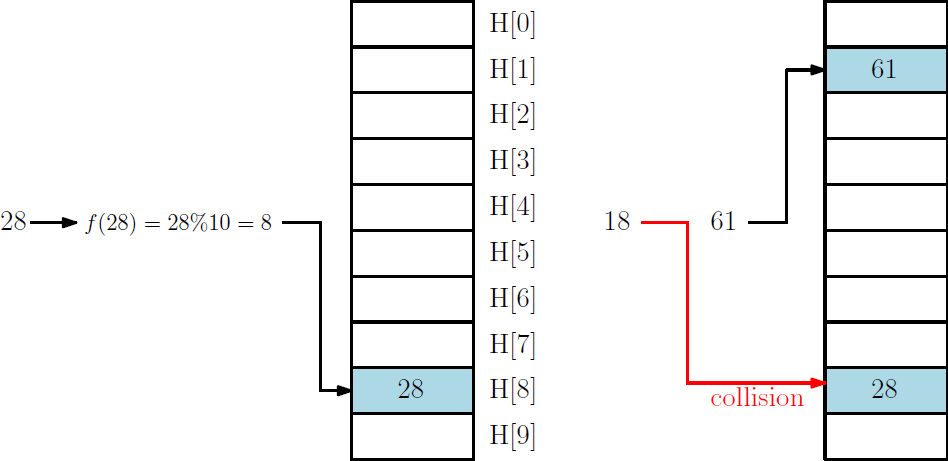
K = 28은 H[f(28)] 슬롯에 저장된다. 즉 H[8]에 저장된다.
근데 K = 18도 H[8]에 저장되어야 한다. 근데 이미 H[8]에는 28이 저장되어 있다.
이런 경우를 충돌이 발생했다고 한다.
충돌이 발생한 경우, 해당 슬롯에 18도 저장할 공간이 더 있으면 그냥 저장하면 되지만,
그렇지 않은 경우 18을 다른 곳에 저장해야한다. 이때 다른 곳을 정하는 방법을 충돌해결방법이라 한다.

hash1

결국 해시테이블에서 중요한 건

테이블을 어떤 방식으로 저장할 것인가? : 파이썬에서는 리스트로 저장
해시 함수를 어떻게 만들 것인가?
충돌 해결은 어떻게 할 것이가?

이렇게 세가지가 성능을 좌우한다.

b. 해시 함수

해시 함수에는 어떤 것들이 있는지 살펴보자.

b-1. 완전 해시 함수

충돌없이 일대일 매핑하는 해시 함수

예를 들어 100개의 슬롯을 가지고 있는 H에 50개의 값을 저장한다고 할때,

100^50=10^100개의 함수가 만들어질 수 있는데,

완전 해시 함수는 100C50 = 10^94이므로,

임의의 함수고 완전 해시 함수일 확률은 10^-6으로 아주 작다…

비현실적이고, 구현하기도 까다롭다.

b-2. c-universal 해시 함수

서로 다른 두 key 값 x, y에 대해 prob(f(x)==f(y)) = c/size(H)이 성립하는 해시 함수

즉 f(x)와 f(y)가 같을 가능성이 c/size(H)인 해시 함수를 c-universal 해시 함수라고 한다.

여기서 c는 0보다 큰 실수 상수이다.

비교적 골고루 매핑하고 완전해시 함수보다 계산하기 쉬워 현실적이다.

b-3. 현실에서 자주 쓰이는 해시 함수들 (key값이 수일 경우)

m = 해시테이블의 크기

mod = 나머지를 구하는 연산

Division : f(k) = (k mod p) mod m (p = 소수)
key 값들의 성질이 잘 알려져 있지 않은 경우에 유용
Folding : key 값이 digit를 나눠 연산하는 형식
k=1254-387-601 이라 할 때,
- shift folding : 두 digit씩 나눠 모두 더한 뒤 mod m ->(12+54+38+76+01) mod m
- boundary folding : 여러 digit로 나눈 후 더하는데 짝수번 조각은 거꾸로해서 더함 ->(12+45+38+67+01)mod m
Mid-Square : key 값을 적당히 연산 후, 그 결과의 중간 부를 떼어나 주소로 이용
- m = 1000, k = 3121 이면, 3121^2=9740641에서 중간에 3digit를 떼어낸 406이 주소가 됨
Extraction : key 값의 각 파트마다 임의의 digit을 떼어내 연결
k=1254-387-601 일 때 1254의 12, 601에서 1을 떼어내 121을 주소로 함

b-4. 현실에서 자주 쓰이는 해시 함수들 (key값이 문자열일 경우)

key[i]는 ascii 코드 값 정도로 하자.

Additive hash : key[i]의 단순 합
Rotating hash : <<, >>(비트 쉬프트) 연산과 ^(xor, exclusive or) 연산을 반복
Universal hash

#좋은 해쉬 함수란?

충돌이 적어야 한다.

빠르게 계산할 수 있어야 한다.

c. 충돌 해결 방법

충돌 해결 방법에는 Open addressing과 Chasing 두 가지 방법이 있다.

c-1. Open addressing : linear probing

예시를 통해 이해해보자!

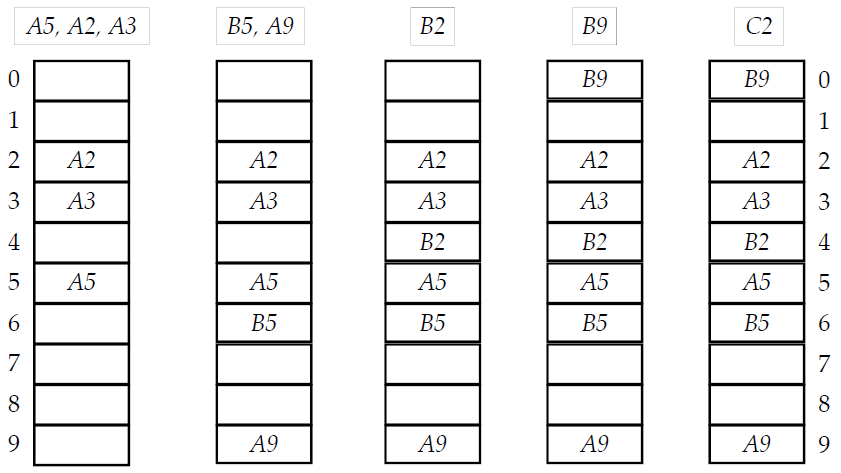
hash2

H의 슬롯에는 값 하나만 저장할 수 있다고 가정
해시 함수에 의해 알파벳 다음 수가 저장될 슬롯이라고 가정하자
open addressing은 내가 들어갈 자리가 이미 차 있다면(충돌이 발생했다면) 아래쪽 슬롯으로 순차적으로 탐색하면서 가장 먼저 만난 빈 슬롯에 저장하는 것이다.
만약 마지막 자리까지 차있다면, 맨 처음 슬롯부터 다시 빈 자리를 찾는다.

c-1-1. open addressing : linear probing 구현

해시 테이블 H의 각 슬롯에는 하나의 아이템을 저장한다고 하자.

아이템은 (key, value) 쌍으로 정의되는데,
key는 아이템을 구분하는데 쓰이므로 서로 달라야 하고, value는 해당 아이템의 정보를 의미한다.

class HashOpenAddr:
    def __init__(self, size=10):
        self.size = size
        self.keys = [None]*self.size
        self.values = [None]*self.size
    
    def __iter__(self):
        for i in range(self.size):
            yield self.keys[i]

c-1-2. 삽입 연산

find_slot(key) :

key값을 갖는 아이템을 찾아 슬롯 번호를 리턴

key값을 갖는 아이템을 못 찾으면, 해당 아이템이 저장되어야 할 슬롯 번호를 리턴

만약 슬롯이 존재하지도 않고 빈 슬롯도 없으면 FULL 리턴

def find_slot(self, key):
        i = self.hash_function(key)
        start = i
        while self.keys[i] != None and self.keys[i] != key:
            i = (i+1) % self.size
            if i == start : return None
        return i

set(key, value) : find_slot(key)를 요긴하게 사용한다!!

key 값을 갖는 아이템이 테이블에 있으면 해당 아이템의 value를 매개변수 value로 수정하고 key 리턴

없다면 새 아이템 (key, value) 삽입하고 key 리턴

테이블에 빈 슬롯이 없어 삽입하지 못하고 key 값을 갖는 아이템도 못찾았으면 FULL 리턴

def set(self, key, value=None):
        i = self.find_slot(key)
        if i == None:
            return None
        if self.keys[i]!=None:
            self.values[i]=value
        else:
            self.keys[i]=key
            self.values[i] = value
        return key

c-1-3. 삭제 연산

remove(key): 어려우니 천천히 살펴보자

key값을 갖는 아이템을 find_slot(key)를 통해 찾고 i에 저장하자
H[i]에 해당 값이 없다면, 삭제할 아이템이 실제로 존재하지 않음을 의미. None 리턴
H[i]가 존재하면, 이 아이템이 삽입 될 때 다른 아이템이 아래쪽으로 밀렸을 가능성을 생각해야한다
- 아래쪽으로 밀린 아이템이 있다면, 해당 아이템들을 연쇄적으로 위로 올려야 한다.
일단 H[i]를 지우고, 아래 쪽 H[j]에 있는 아이템들을 H[i]로 이동할지 결정해야 한다.
H[j]의 키 값을 해시함수 결과값을 k로 하자. (즉 원래 들어가야했을 자리를 k라고 하자)
이때 k가 i<k<=j 면 H[j]를 H[i]로 옮기면 안된다!
왜냐면, 원래 위치 k가 j에 있게 된 이유가 i 때문은 아니라는 것을 의미하기 때문이다.
즉 i에 밀려 j로 간 게 아니다.(다른 이유로 밀렸을 것이다.)
또한 해시 테이블은 원형이기 때문에, i > j 일 가능성도 있다
그러면 j가 한바퀴를 돌아 j<i<k, k<=j<i 이 두 구간도 옮기면 안된다.
(i때문에 k에 있어야 할 게 j로 간 것이 아니므로)
이 세가지 경우가 아니라면, H[j]를 H[i]로 옮긴다.
(결국 옮기는 경우는 두가지다.
- k값이 i와 같거나(i 때문에 j로 밀림)
- k<i<j 이거나 (k에 이미 값이 있어서 내려왔는데 i에도 값이 있어 j로 간 경우))
그러면 이제 H[j]가 빈 슬롯이 되니 다시 4번으로 돌아가 반복한다.

def remove(self, key):
        i = self.find_slot(key)
        j = i
        if i == None : return None
        if self.keys[i] == None : return None
        while True:
            self.keys[i]=None
            self.values[i]=None
            while True:
                j = (j +1) % self.size
                if self.keys[j] == None:
                    return key
                k = self.hash_function(self.keys[j])
                if not (i<k<=j or j<i<k or k<=j<i):
                    break
            self.keys[i] = self.keys[j]
            self.values[i] = self.values[j]
            i = j

c-1-4. 탐색 연산

search(key) :

key 값을 갖는 아이템을 찾아 value(혹은 key)값을 리턴

없으면 None 리턴

def search(self, key):
        i = self.find_slot(key)
        if i != None:
            if self.keys[i] != None:
                return self.keys[i]
        return None

c-2. Chaining

슬롯에 값 하나만 저장하는게 아니라, 각 슬롯마다 연결리스트를 연결하여 슬롯 당 이론적으로 무한한 갯수 값을 저장하는 방법

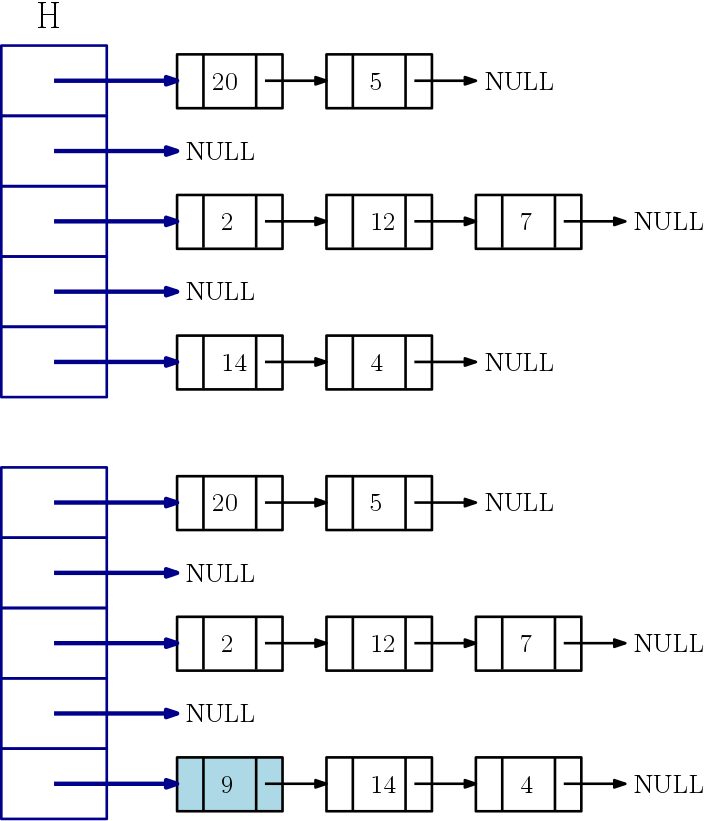
hash3

class HashChain:
	def __init__(self, m):
		self.size = m		# 슬롯의 갯수 m
		self.H = [None] * self.size
		
	def hash_function(self, key):
		return f(key)	# return hash value for key
	
	def find_slot(self, key):
		# chaining이므로 빈 슬롯을 찾을 필요없이 해시함수값을 리턴
		return self.hash_function(key)

	def set(self, key, value):
		i = self.find_slot(key)
		v = self.H[i].search(key)
		if v == None: # key 값을 갖는 노드가 없다면 삽입연산
			self.H[i].pushFront(key, value) # (key, value) 노드를 head 노드 위치에 삽입!
		else: # 기존의 key값을 갖는 노드가 있으므로 value값 수정
			v.value = value
	
	def remove(self, key):
		i = self.find_slot(key)
		v = self.H[i].search(key)
		if v == None return NOTFOUND
		else:
			self.H[i].deleteNode(v)

mudura

Computer ScienceData Structure